What is Quantum Computing and How It Differs from Classical Computing

Quantum computing is a new paradigm of computation that leverages the principles of quantum mechanics—such as superposition, entanglement, and interference—to process information in fundamentally different ways from classical computers.
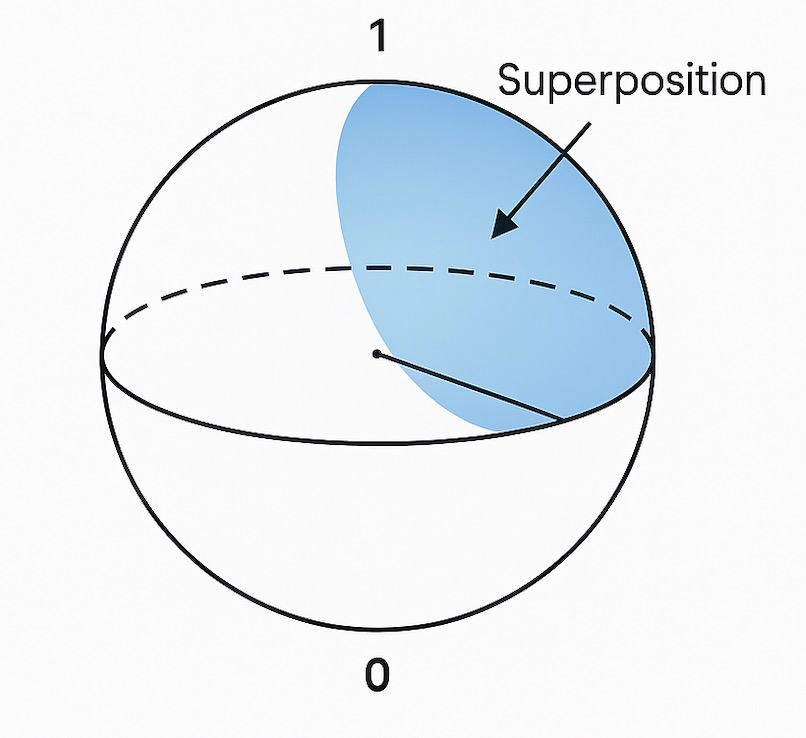
While classical computers represent data as bits that are either 0 or 1, quantum computers use quantum bits, or qubits, which can exist in multiple states simultaneously. Thanks to following properties, quantum computers can explore many possible solutions at once, making them potentially far more efficient for certain complex problems.
| Quantum Concept | Explanation |
|---|---|
| Superposition | A quantum system can exist in multiple states at once (e.g., a qubit being both 0 and 1 simultaneously). |
| Entanglement | Two or more quantum particles are correlated in such a way that the state of one instantly affects the state of the other, regardless of distance. |
| Interference | When multiple quantum states overlap, their probabilities can reinforce (constructive interference) or cancel each other out (destructive interference). |

The concept of quantum computing emerged from the idea that physical systems at the quantum level can perform computations by naturally exploiting quantum phenomena, offering new ways to solve tasks like optimization, cryptography, and molecular simulation that are intractable for traditional systems.
How Quantum Computing Works: A Simple Overview
It may be hard to find content that explains the technology in an easy-to-understand way. Here, I provide a simplified summary of the concept for better understanding.
A qubit, or quantum bit, is the basic unit of quantum information. Unlike a classical bit, which can be either 0 or 1, a qubit can be in a superposition of both states simultaneously.
Each developer uses different methods to leverage(implement a qubit) quantum superposition (such as electron spin-based, photon polarization-based, etc.), but to help with a basic understanding of the technology, let's explain the quantum computing process using electron spin-based technology.
Since we’re not experts, we’ll focus only on the general concept.
0. What is Electron Spin?
Electron spin refers to a fundamental property of electrons that gives them a magnetic moment, much like a tiny magnet. It’s a type of intrinsic angular momentum that is quantized, meaning it can only take on specific values. In quantum mechanics, spin is not about physical spinning but represents a quantum property that influences how particles interact with magnetic fields.
There are two possible states for electron spin:
- Spin-up (↑\uparrow↑): The electron’s spin is aligned with an external magnetic field.
- Spin-down (↓\downarrow↓): The electron’s spin is opposite to the magnetic field.
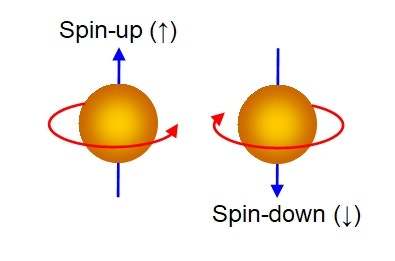
Thus, in electron spin-based quantum computing, the spin-up state is defined as the value 1, and the spin-down state is defined as the value 0. This assignment allows the electron’s spin states to serve as quantum bits (qubits), where each qubit can exist in a superposition of both 0 and 1 simultaneously, enabling quantum parallelism.
Move on to the Quantum Computing Works.
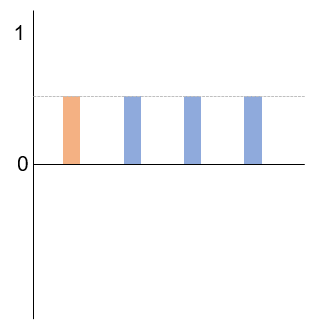
1. Superposition
- In this step, qubits are put into superposition, meaning they can represent multiple states simultaneously.
- For example, applying a Hadamard gate1 to a qubit in state 0(spin-down) creates an equal superposition of 0(spin-down) & 1(spin-up)
- If you apply this gate to multiple qubits, you create superposition for all combinations, allowing quantum computers to handle many possibilities at once.
ex) Superpositioning of initialized 4 Qubits : (0, 0, 0, 0) → (0.5, 0.5, 0.5, 0.5)
* Number shows probability of Qubit State : 0.5 = 0 (spin-down) * 50% + 1 (spin-up) * 50%
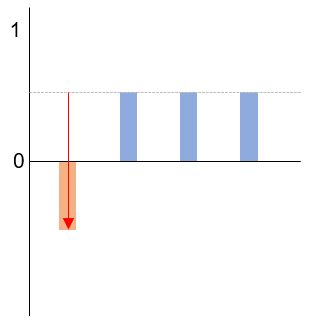
2. Phase Change
- This step uses a phase flip to mark the correct solution by changing the phase of the corresponding qubit.
- This step doesn’t change the probabilities directly but sets up the next stage for interference, where the marked states will be differentiated.
ex) Phase Change of 4 Qubits : (0.5, 0.5, 0.5, 0.5) → (-0.5(Correct Answer), 0.5, 0.5, 0.5)
* I hope you understand the concept of attaching a phase by adding a negative sign.
3. Amplitude Amplification
- In this step, the probability of the correct state is amplified using interference. The goal is to increase the amplitude of the correct solution while reducing the amplitudes of wrong ones.
- Applying the amplitude amplification operation flips the state around the average (the “reflection” process), increasing the amplitude of 1 and decreasing the amplitude of 0.
- After enough repetitions, the amplitude of the correct state grows, making it more likely to be measured.
ex) amplification of 4 Qubits : (-0.5(Correct Answer), 0.5, 0.5, 0.5) → (0.25 + (0.25-(-0.5)), 0.25 + (0.25-(0.5)), 0.25 + (0.25-(0.5)), 0.25 + (0.25-(0.5)))
→ (1,0,0,0)

4. Measurement (측정)
- Finally, the qubits are measured, and the system collapses to one of the possible states. Due to amplitude amplification, the correct state will have a higher probability of being measured.
- After sufficient repetitions of the earlier steps (oracle and amplitude amplification), We can get the answers
ex) Measurement of 4 Qubits : (1, 0, 0,0), First is the answer!
Detailed Quantum Computers‘ Advantages
Classical computers are based on bits, which can either be 0 or 1. For example, with 4 bits, a classical computer can represent 16 different combinations (from 0000 to 1111), and it processes these combinations one at a time. To handle all 16 possibilities, the computer needs to go through each one sequentially.
On the other hand, quantum computers use qubits (quantum bits), which can exist in both 0 and 1 states simultaneously due to the principle of quantum superposition. This allows quantum computers to represent multiple possibilities at once. For example, with just 4 qubits, a quantum computer can process all 16 combinations simultaneously, instead of sequentially.

Quantum Computing Advantage
- Increased Computational Power: The more qubits you add, the more possibilities you can represent and compute simultaneously. For instance, with 10 qubits, a quantum computer can represent 1,024 different combinations, and with 20 qubits, it can handle over a million combinations at once. This leads to a significant increase in computational speed and efficiency.
- Exponential Growth: For each additional qubit, the number of possible states grows exponentially. For example, a 53-qubit quantum computer can represent and process approximately 1 quadrillion (9007 trillion 1993 billion) combinations simultaneously. This exponential growth allows quantum computers to solve problems that are practically impossible for classical computers, even with billions of bits.
Real-World Example
In 2019, Google’s Sycamore quantum processor, with 53 qubits, achieved a breakthrough by performing a specific computation in 200 seconds. This computation would have taken the world’s most powerful supercomputer, IBM Summit, over 10,000 years to complete. Although IBM researchers argued that the problem was particularly suited for quantum computation, this achievement still highlighted the significant speed advantage that quantum computers have over classical systems for specific tasks.
Let’s continue with the industry analysis.
- A Hadamard gate is a basic quantum logic gate that takes a qubit in a definite state (spin up or down) and turns it into a superposition of both states with equal probability. ↩︎